Hablemos de impedancias (II)
-69939.jpg)
Como continuación del artículo anterior, seguiré deconstruyendo en éste el concepto de impedancia. Veremos por qué es tan importante en según qué casos.
Un poco de base matemática
Para entender los siguientes apartados, recordemos el nombre de un importantísimo matemático y físico francés: Joseph Fourier. La transformada matemática que desarrolló (y que lleva su nombre), nos permite descomponer cualquier función (señal) como una suma, que puede ser infinita, de senos y/o cosenos. Es decir, tenemos una herramienta poderosísima que nos permite transformar una señal del dominio del tiempo al de la frecuencia (y viceversa), de tal manera que podemos conocer cuáles son sus componentes frecuenciales y en cuáles de ellos se acumula la mayor cantidad de energía. Quedémonos con esta información para más adelante.
Lo que la lógica nos dice
En el artículo anterior, describimos toda línea de transmisión como una suma infinita de elementos infinitesimales que se pueden modelar como un conjunto de resistencias, capacidades e inductancias. (Referirse al artículo para más detalles).
Imaginemos ahora una señal senoidal de frecuencia 1 MHz. Dicha señal se repite infinitamente cada microsegundo (período). Asumamos ahora que inyectamos esta señal en una pista microstrip cualquiera de una PCB cualquiera construida con FR-4 (simplificando su coeficiente dieléctrico como 4). El cálculo cambiaría ligeramente si usáramos una línea stripline o de otro tipo.
La velocidad de propagación de tal señal en esa pista será la mitad de la velocidad de la luz. Dicho de otra manera: 150 mm/ns. Observemos que, en realidad, la señal se propaga usando el dieléctrico como soporte, no el cobre. Nuestra señal necesitaría entonces 150 metros de pista para completar un período completo.
Es evidente que ninguna PCB llega a tales dimensiones (ni de lejos). Se puede decir que la longitud de cualquier pista de la PCB será mucho menor que un ciclo de la señal. Es más, es correcto simplificar que el valor que toma la señal en un instante de tiempo dado, es el mismo en toda la longitud de la pista.
A efectos de propagación, la lógica nos dice que, cuando la longitud de la pista es mucho menor que la máxima frecuencia de la señal (o que la longitud de onda más larga que compone dicha señal), se puede considerar una señal de corriente continua (DC).
Evidentemente, cuanto más alta es la frecuencia de la señal, menos se cumple el razonamiento anterior y la pista se aproxima más al comportamiento de una línea de transmisión.
Veamos dónde está el límite.
¿Cuándo debe considerarse una pista una línea de transmisión?
IPC nos da un método para calcular la longitud límite a partir de la cual debemos considerar una pista como línea de transmisión cuando tratamos con señales digitales.
Las señales digitales son, idealmente, trenes de pulsos cuadrados a una determinada frecuencia. Sin embargo, no será la frecuencia de dicha señal el factor clave que determine si una señal es de alta frecuencia o no, sino la velocidad a la que esa señal conmuta. El tiempo de subida (o de bajada), siempre tendrá componentes frecuenciales más elevadas que la frecuencia de la propia señal, como es lógico.
Haciendo uso de la transformada de Fourier, y simplificando, el método de IPC llega a la conclusión de que la máxima componente frecuencial de una señal digital se puede aproximar por:
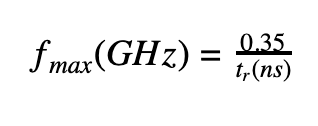
Siendo tr el tiempo de subida del pulso desde el 10% al 90% del valor máximo de la señal.
Definición de tiempo de subida (Fuente)
En realidad, los pulsos tienen infinitas componentes frecuenciales. Lo que hacemos con esta aproximación, es quedarnos con aquéllas en las que se concentra la mayor parte de la energía de la señal.
En el caso de que ignoremos el tiempo de subida de nuestra señal, podemos aproximarlo como el 7% del período total de la señal. Esto nos da:
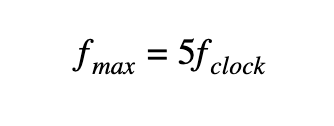
Una vez conocida la frecuencia máxima de nuestra señal, definimos la longitud límite como:
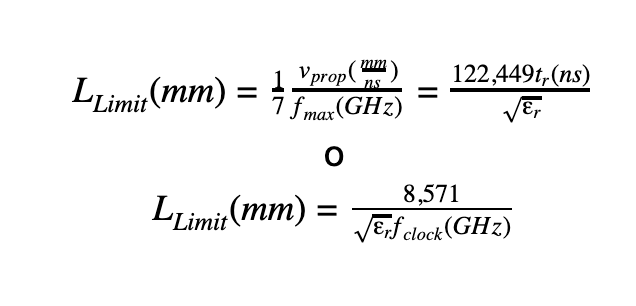
Usamos una u otra ecuación dependiendo de si conocemos o no el tiempo de subida.
Como se observa, el criterio utilizado es muy conservador, puesto que toma 1/7 de un período de la señal para tener una salvaguarda amplia. Pueden considerarse otros criterios más o menos conservadores. El arriba descrito, funciona eficientemente, según mi experiencia en años de diseño.
Consecuencias
A efectos prácticos, toda pista que supera la longitud límite debe tratarse como una línea de transmisión. La principal implicación es que se hace necesario un control de la impedancia característica de tales líneas para evitar reflexiones que serían nefastas para la integridad de la señal así como para la compatibilidad electromagnética.
En la primera parte de esta serie de dos artículos, expliqué cómo podemos conseguir este control de una manera muy sencilla con ayuda de Altium.
Ejemplo práctico
Tomemos como ejemplo las líneas de datos del estándar USB 2.0. Tomemos como velocidad de transmisión de datos 400 Mbps (aunque podría llegar a 480 Mbps). Se transmiten 2 bits por cada ciclo de reloj, lo cual nos dice que la frecuencia de éste es 200 MHz.
Si tomamos como material dieléctrico FR-4 de coeficiente dieléctrico 4, obtenemos una longitud límite de 21 mm.
Esto significa que, si somos capaces de mantener las líneas de datos de USB 2.0 más cortas que 21 mm, no se necesita ninguna precaución. Cualquier geometría de línea funcionará.
Si, por el contrario, superamos esos 21 mm, necesitamos tener control sobre la impedancia de dichas líneas.
Conclusión
Como podemos observar, un estándar muy común (USB 2.0) exige en casi todos los casos control de impedancia.
Señales que, a priori, son de baja frecuencia atendiendo a su período, precisan de estricto control de impedancia debido a sus rápidos tiempos de conmutación, que son el factor determinante.
En este artículo se proporciona un método para determinar cuándo una pista se comporta como una línea de transmisión y explica cómo actuar en tal caso.